NIR Water Vapor Algorithm

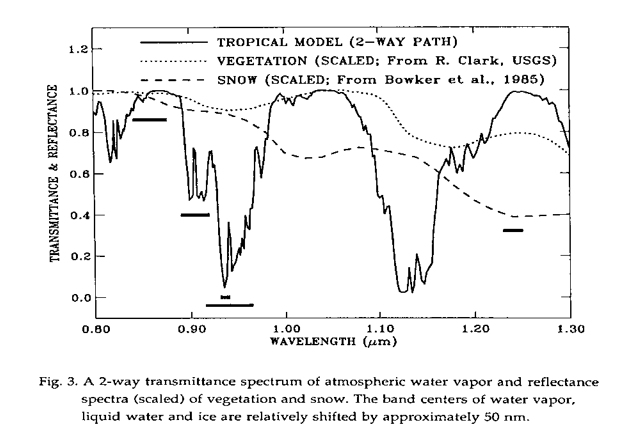
MODIS is an instrument on the EOS polar orbiting satellite platforms designed to measure biological and physical processes on a global scale every 1 to 2 days. It is a 36-channel scanning radiometer covering the spectral region 0.4 - 15 µm . Five near-IR MODIS channels are useful for remote sensing of water vapor. The positions and widths of these channels are given in Table 1.

Table 1: Positions and widths of five MODIS near-IR channels used in water vapor retrievals.

Two atmospheric water vapor transmittance spectra for the Tropical and SubArctic Winter Models in LOWTRAN7 (Kneizys et al., 1988) with a solar zenith angle of 45 degrees and a nadir-looking geometry are also shown in Figure 1.

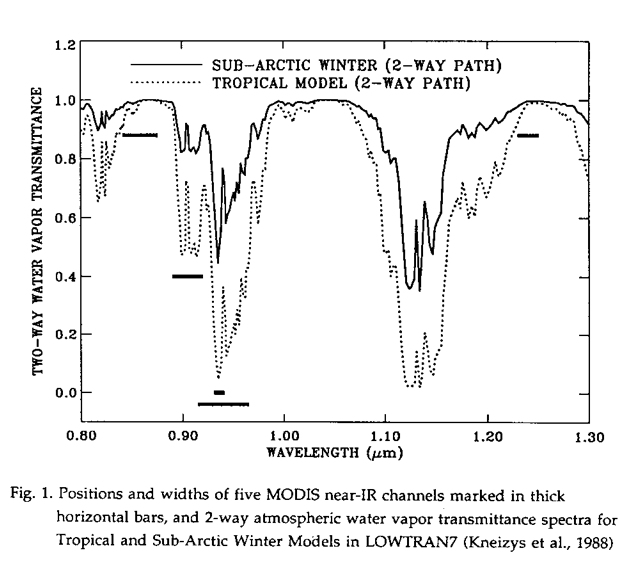
The channels at 0.865 and 1.24 µm are non-absorption channels present on MODIS for remote sensing of vegetation and clouds. The channels at 0.935, 0.940, and 0.905 µm are water vapor absorption channels with decreasing absorption coefficients. The strong absorption channel at 0.935 µm is most useful for dry conditions, while the weak absorption channel at 0.905 µm is most useful for very humid conditions, or low solar elevation.

The Water Vapor remote sensing method is based on detecting the absorption by water vapor of the reflected solar radiation after it has transferred down to the surface and back up through the atmosphere. The total vertical amount of water vapor can be derived from a comparison between the reflected solar radiation in the absorption channel, and the reflected solar radiation in nearby non-absorption channels. Detailed descriptions of the remote sensing method have been published (Kaufman and Gao, 1992; Gao and Goetz, 1990). Below are abbreviated descriptions of the remote sensing method. General descriptions of remote sensing of cloud, aerosol, and water vapor properties from MODIS have been given by King et al. (1992).

The solar radiation between 0.86 and 1.24 µm on the Sun-surface-sensor path is subjected to atmospheric water vapor absorption, atmospheric aerosol scattering, and surface reflection. In order to derive column water vapor from measurements of solar radiation reflected by the surface, the absorption and scattering properties of the atmosphere and the surface near 1 µm must be taken into consideration.

Atmospheric Absorption and Scattering in the 0.86-1.24 µm Range

The radiance at a downward-looking satellite sensor can be written (Hansen and Travis, 1974, Fraser and Kaufman, 1985), in a simplified form, as

LSensor(λ) = LSun(λ) T(λ) ρ(λ)+ LPath(λ)                                      (1)

where λ is the wavelength, LSensor(λ) is the radiance at the sensor, LSun(λ) is the solar radiance above the atmosphere, T(λ) is the total atmospheric transmittance, which is equal to the product of the atmospheric transmittance from the Sun to the Earth's surface and that from the surface to the satellite sensor, ρ(λ) is the surface bidirectional reflectance, and LPath(λ) is the path scattered radiance. Eq. (1) is simplified in a sense that photons that are reflected from the surface more than once are being ignored. This feedback mechanism involves back scattering to the surface by the atmosphere. The feedback effect is usually small, because aerosol optical thicknesses are typically small in the near-IR region. The first term on the right side of Eq. (1) is the direct reflected solar radiation. LDirect is used to represent this component. LSensor(λ)/ LSun(λ) is defined as the apparent reflectance ρ*(λ).

The T(λ) contains information about the total amount of water vapor in the combined Sun-surface-sensor path. LSun(λ) is a known quantity. Near 1 µm , Rayleigh scattering is negligible and the main contribution to LPath(λ) is scattering by aerosols. LPath(λ) in the 1 µm region is usually a few percent of the direct reflected solar radiation. Because most aerosols are located in the lower 2 km of the atmosphere and the same is true for atmospheric water vapor, the single and multiple scattered radiation by aerosols is also subjected to water vapor absorption. As a result, LPath(λ) contains water vapor absorption features (Gao and Goetz, 1990).

We assume that LPath(λ) can be treated approximately as an unspecified fraction of direct reflected solar radiation when the aerosol concentrations are low. This assumption allows the derivation of column water vapor amounts from satellite data without the need to model single and multiple scattering effects. In the following we describe in detail the water vapor retrieval algorithm for cloud free pixels. A similar algorithm is applicable for retrievals over cloudy pixels.

Surface Reflectances Near 1 µm

Most land is either covered by soils, rocks, vegetation, snow, or ice. Figure 2 shows reflectance curves of five major types of soil (Condit, 1970; Stoner and Baumgardner, 1980). The reflectances between 0.85 and 1.25 µm change approximately linearly with wavelength. Similar linearity is observed in reflectance spectra of common rocks and minerals. The largest deviation from linearity is observed in reflectance spectra of iron-rich soils and minerals. These materials have broad electronic bands, which are related to the Fe3+ transition and are centered near 0.86 µm. Curve 3 in Fig. 2 shows such a broad band feature in the spectral region between approximately 0.8 and 1.25 µm.

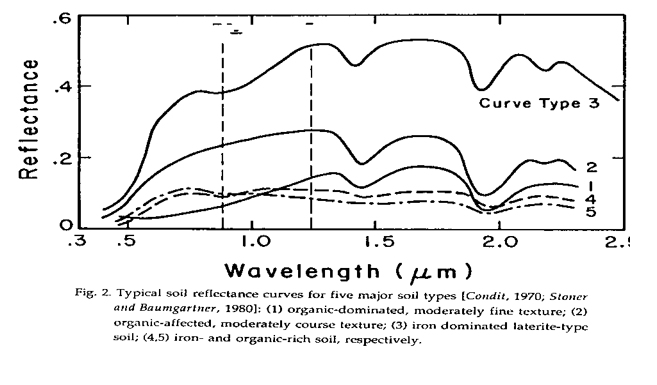
Figure 3 shows vegetation and snow reflectance spectra (Bowker et al., 1985). The vegetation spectrum has liquid water bands centered at approximately 0.98 and 1.20 µm. The snow spectrum has ice absorption bands centered approximately at 1.04 and 1.24 µm. For comparison, Fig. 3 also shows a calculated water vapor transmittance spectrum. The positions of water vapor, liquid water and ice absorption bands are shifted relative to each other. The shifting of the vibrational bands is due to increases in intermolecular forces as the water molecules become more organized in the liquid and solid states.